Intuition behind Power of 2 Choices Load balancing

One of the hardest parts of balancing load across many targets is keeping an accurate view of their load. We have to check all the targets; this is expensive. Also, the process of checking is not instantaneous, which leads to stale data which in turn causes request herding. What if we assign a request to a random target? This works surprisingly well but causes hotspots, which is not ideal. A variant of this is where we select 2 targets at random and then assign the request to the one with less load, which works even better. This is called the Power of 2 Choices balancing.

This has been studied in Maths as the Balls & Bins problem. Where we place balls into bins, where a bin can house any number of balls. From here, we get that the typical max load on a target is exponentially better with 2 choices, i.e. $\mathcal{O(\frac{\log n}{\log\log n})}$ for random and $\mathcal{O(\frac{\log\log n}{\log d})}$ for $d$ random choices, for 2 this will be $\mathcal{O(\log \log n)}$. From this result, we can also see that going from 1 to 2 improvement is far better than selections of 3 or 4, which are only marginally better. But it is not obvious intuitively, since we are still selecting the two targets randomly. This same exponential gap underlies why data structures like cuckoo hashing work so well: having two random choices dramatically reduces collisions and spreads keys more evenly.

Here is a visualisation of how the Power of 2 choices approach perform better, as you can see in the gif, the load appears more uniform as the number of requests increases.

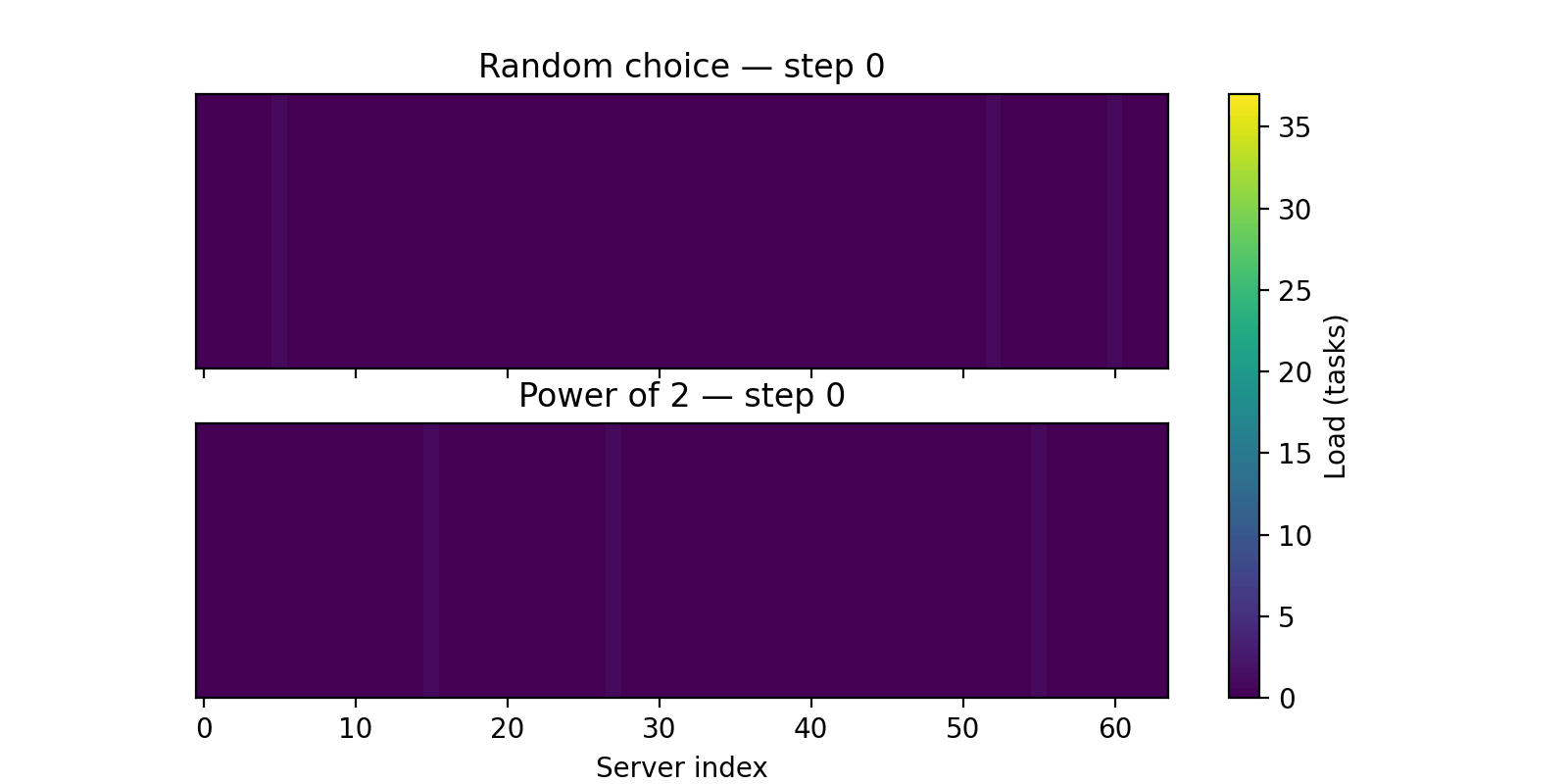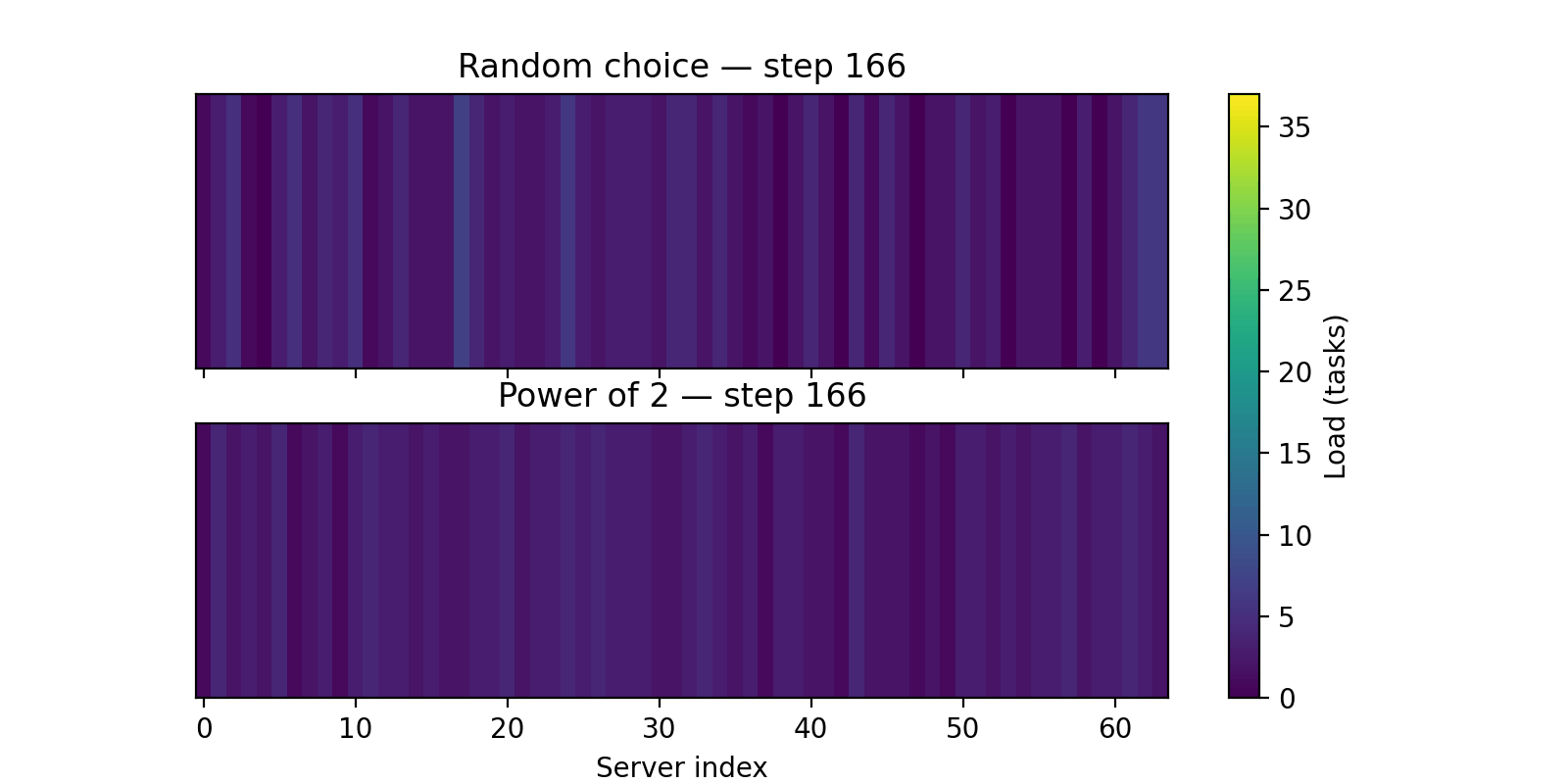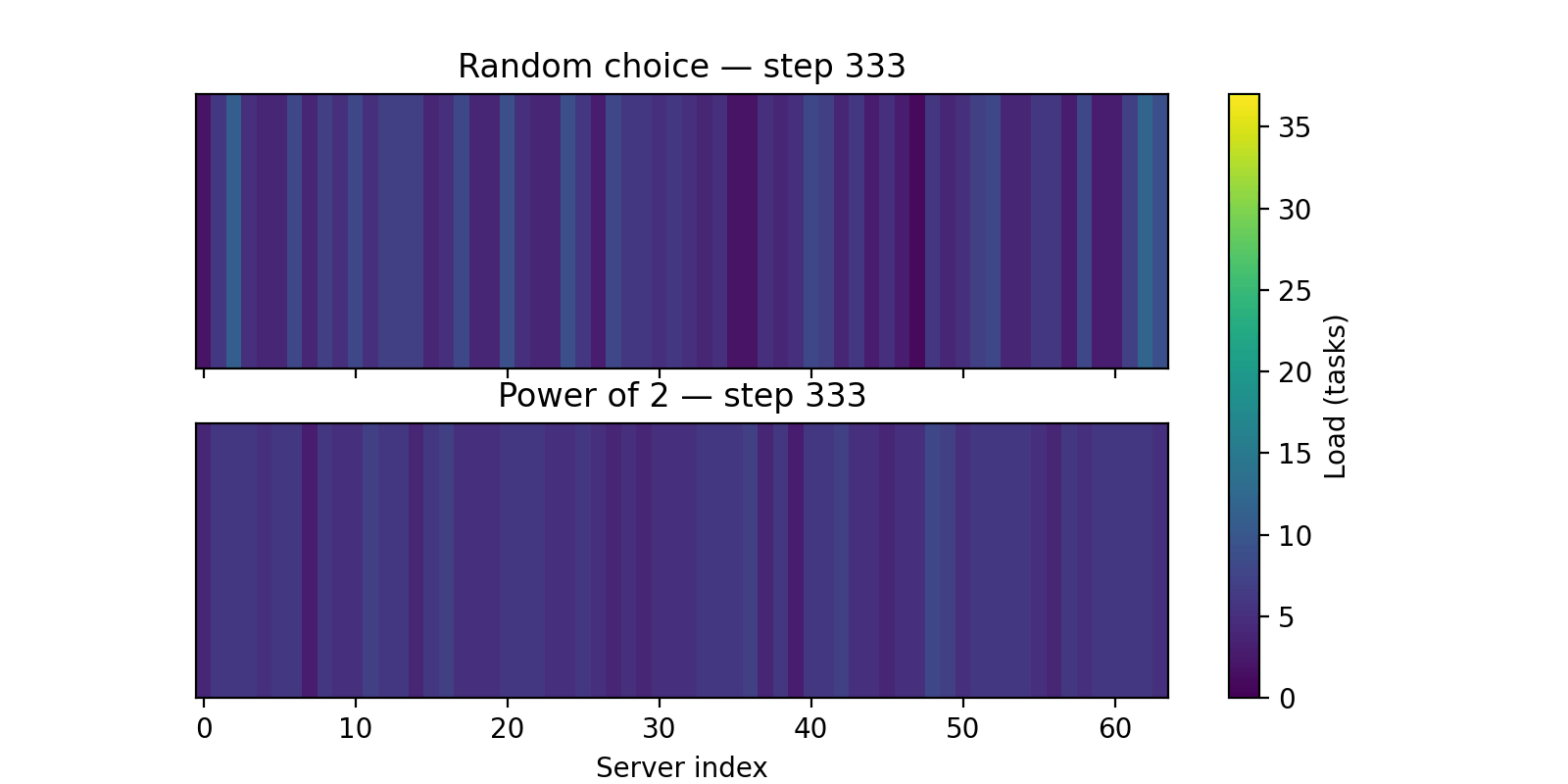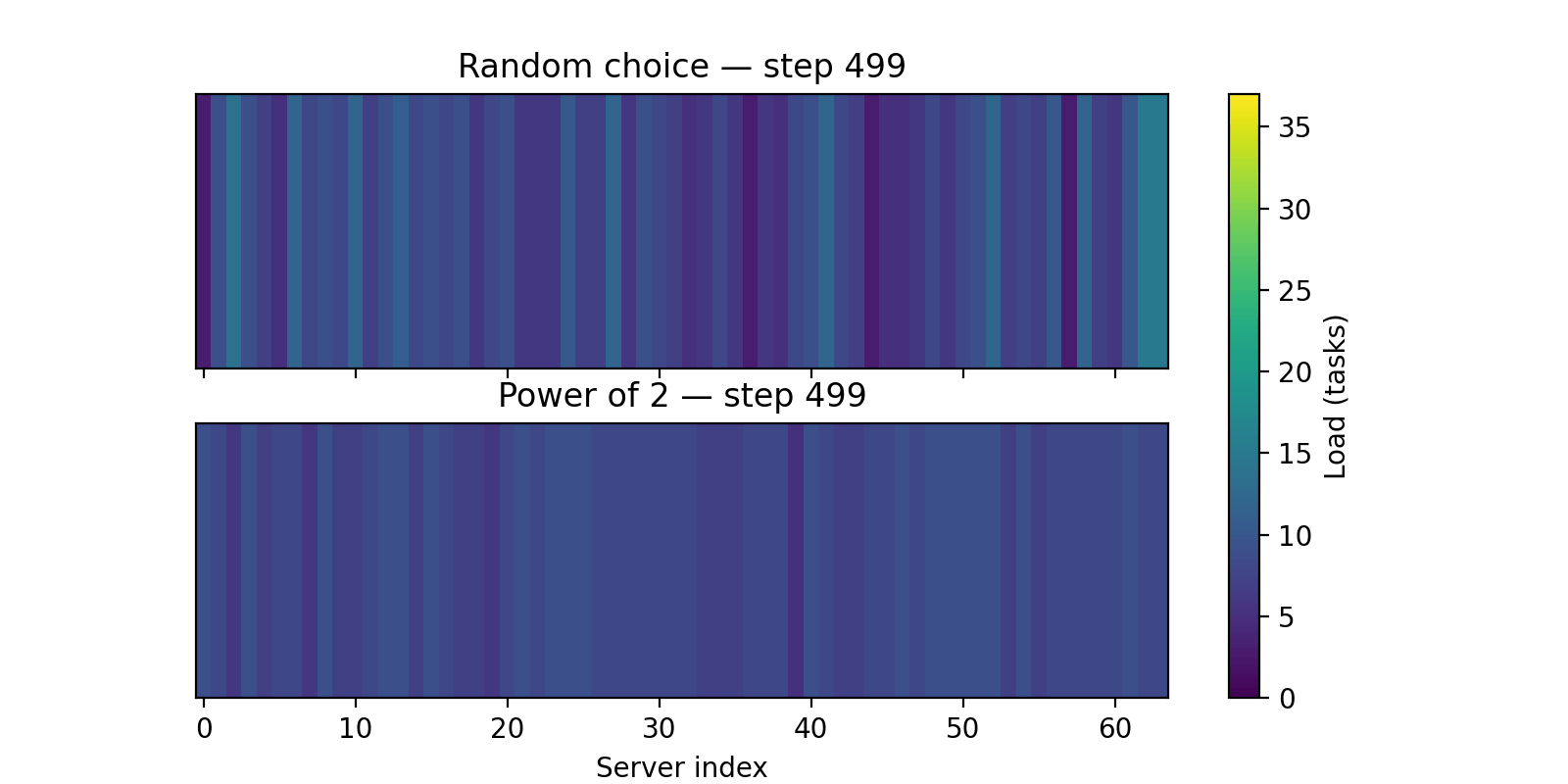
If you want to go deeper into the practical side of these tradeoffs, Tyler McCullen’s talk “Load Balancing is Impossible” and Mark Booker’s Blog Post are excellent resources.

I recently found a UWaterloo slide about this that had a very intuitive explanation of this. Say in our servers, $N_k$ servers are already at max load out of a total $n$ servers, say max load is $k$. The probability that the max load grows is just $N_k/n$ since we can only choose one target. But when we get to choose two targets, what is the probability that the max load grows? What would it take to make $k+1$? We will have to choose two targets that are already at $k$, since if only one is at $k$, the other target will be selected, and max will not increase. Now, what is the probability that two targets are at max and we choose both of them is $(N_k/n)^2$.

Here, $N_k$ would already be small. Furthermore to increase the max even more from $k+1$ to $k+2$, the number of servers with max load would have fallen even more, call it $N_{k+1}$, the probability will be $(N_{k+1}/n)^2$ which is event tinier than moving from $k$ to $k+1$. This is why the tail of max load in case of 2 choices falls very rapidly, since with every iteration the probability of increasing the max falls faster than the single choice method.

Let’s go through with an example

• Say we have $n/4$ targets with a max of $4$ requests each, the probability of selecting two of these is $1/16$.
• Now we should expect only $n/16$ targets to have the max $5$ requests, and then only $n/256 = n/(2^{2^3})$ targets with max $6$ requests
• This amounts to $\frac{n}{2^{2^{k-3}}}$ for a max of $k$ requests.
• To find the upper bound of $k$ at a fixed $n$ we can set the $N_k$ to the minimum $1$. This will give us $k = \mathcal{O(\log \log n)}$